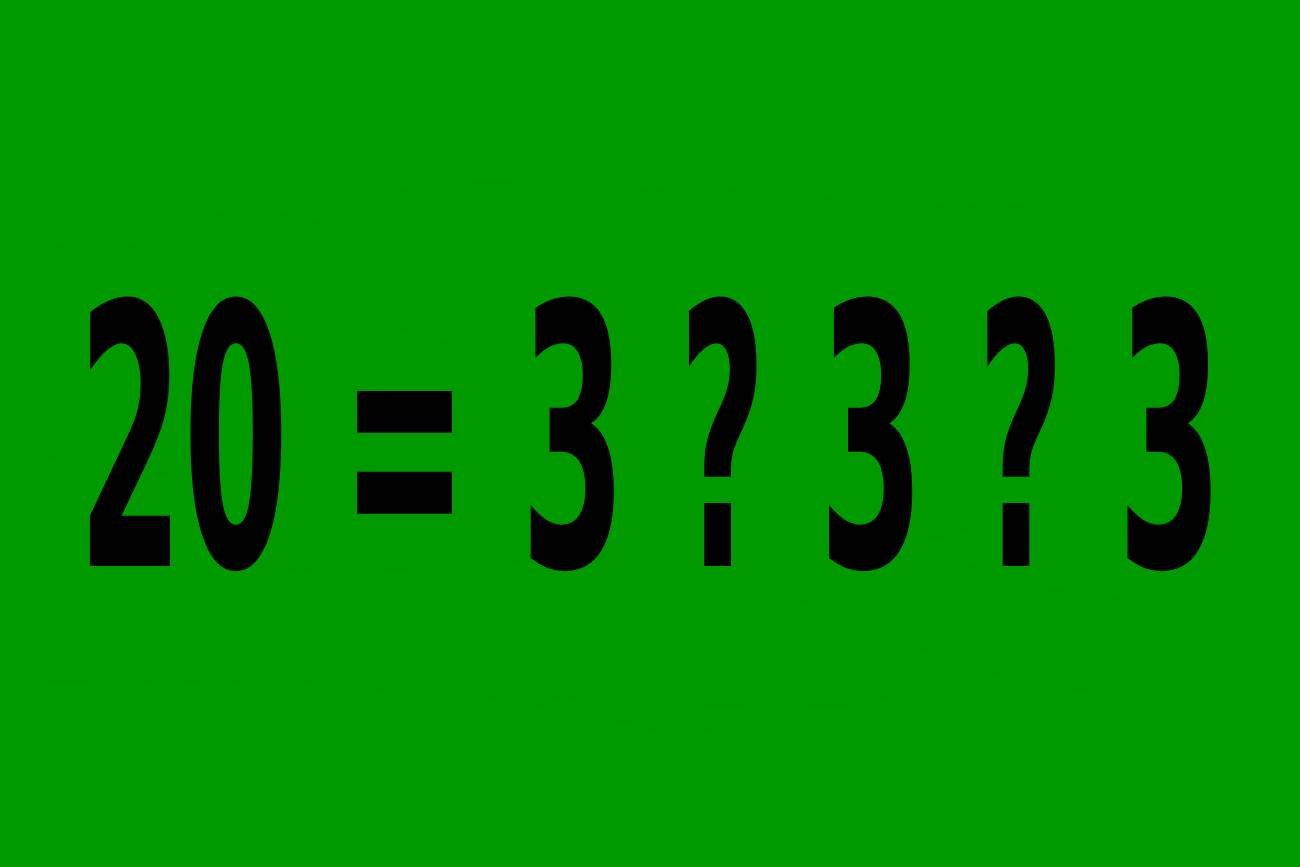
W chwili przerwy albo dojazdu do pracy małe wyzwania matematyczne mogą być bardzo dobrym sposobem, by rozruszać i zająć mózg. Tym bardziej, jeśli zmusimy go do kreatywnego wykorzystania posiadanej wiedzy.
Jak z trzech niedopasowanych elementów i zestawu narzędzi stworzyć pasującą całość? To wbrew pozorom nie jest wyzwanie dla kogoś składającego szwedzkie meble, a temat dzisiejszej zagadki.
Wyobraźmy sobie, że otwieramy szafę i patrzymy się na komplet narzędzi, którymi można budować matematyczne równania. Niektóre znamy i stosujemy często, inne trochę się kurzą. Trzeba zakasać rękawy, żeby wykombinować, jak użyć je do następującego wyzwania:
Masz do dyspozycji: trzy cyfry 3 oraz pełen zestaw matematycznych znaków bez ograniczeń (plus, minus, pierwiastki, potęgi, nawiasy, funkcje…) musisz zbudować wzór, dzięki któremu wyjdzie suma 20.
Znaki zapytania na obrazku są tylko dla wizualizacji problemu, nie musicie wstawiać symboli dokładnie w ich miejsca.
Dasz radę? Podpowiadamy, że rozwiązań jest kilka, ale zakładamy te najprostsze. Odpowiedź znajdziesz poniżej.
Odkładamy mentalne śrubokręty i patrzymy, co nam wyszło. Żeby z zestawu trójek zrobić 20, potrzebujemy jedynie czterech elementów:
20 = (3+3)÷0,3
Jeśli drapiecie się w głowę, to już wyjaśniam - stawiamy przecinek, czyli separator dziesiętny przed 3 i uzyskujemy 0,3. W zagadkach możecie spotkać się z jeszcze formą zapisu ",3" albo ".3" w zależności od kraju.
Jak wspominaliśmy, to nie jest jedyne rozwiązanie. Jeśli możemy skorzystać z pełnego zestawu matematycznych narzędzi, to inżynierowie wykręcą bardziej skomplikowane równania z użyciem trzech cyfr. Nam wystarczy jednak… silnia. Czyli iloczyn wszystkich liczb naturalnych dodatnich nie większych niż n. Zapisujemy ją wykrzyknikiem.
n = 3 n! = 6
Korzystając z silni, możemy zrobić następujący wzór:
20 = (3!)!÷(3! * 3!)
20 = 6!÷36
20 = 720÷36
Jeśli znaleźliście jeszcze jakieś zaawansowane wzory i pokręcony pomysły, to gratulacje!
Jeśli macie ochotę jeszcze pogłówkować, zapraszamy do kolejnego matematycznego ćwiczenia.